-Vanshika Paharia
Everyone hates rain. It dampens fun and isn’t always romantic. Especially in a sport like cricket, rain is a downer. Unlike football matches, cricket matches cannot be carried out in rain because of visibility issues, playing conditions, game duration and an unfair advantage that rain may provide to the other team. In countries like UK, rain is a frequent guest that results in match suspensions, delays and halts. Sometimes, the rain is so prolonged that covering the ground with sheets is not feasible. Matches are delayed and suspended due to a few other issues too, rain being the most common one. This was a major problem for limited over matches.
I simply gotta march
My heart’s a drummer
Don’t bring around a cloud
To rain on my parade!
-Don’t Rain on my Parade, Barbra Streisand
Before 1992, a lot of methods were used to resolve cricket matches that were affected by rain. The Average Run Rate and Most Productive Overs Method were the most used methods. Although simple, both methods had intrinsic flaws that produced unfair revised targets for the team after the game resumed. 2 British statisticians, Frank Duckworth and Tony Lewis devised a method called the D/L Method in 1992 when rain left South Africa with an unfair revised target of 21 runs from 1 ball. Now famously known as the Duckworth-Lewis-Stern Method, it was adopted by ICC in 1999 for one day matches.
I recall hearing Christopher Martin-Jenkins on radio saying ‘surely someone, somewhere could come up with something better’ and I soon realized that it was a mathematical problem that required a mathematical solution.
Frank Duckworth

Involving mathematics and statistics to the core, D/L system has confused and troubled cricket lovers and fans since inception. With an aim to explain the calculation behind the method in an easy to comprehend manner, the article will hopefully be fun for you.
THE CONCEPT OF “RESOURCES’: According to the D/L Method, 2 resources exist that are closely correlated to the score that a team may make.
- The number of overs that are left in the match
- The number of wickets lost
The D/L Method calculates the percentage of resources left using these two resources. E.g. If 50 overs and 10 wickets are remaining, percentage of resources is 100%. A pre published table is available that shows the percentage of resources for all 10 wickets and 50 overs. The actual resource values are calculated using a computer software. The target for the team batting 2nd (Team 2) is calculated up or down as a percentage of the resources used by Team 1 to reach a certain score.

CALCULATION OF THE TARGET:

This is the version of D/L System used commonly for one day and first-class matches.
Team 2’s par score is the score that is considered on the same level as the number of runs scored by Team 1 in the first innings. Team 1’s score is the number of runs scored in the first innings. Generally, the result of this formula is a non integer. Thus, the par score is said to be rounded down and the target score is rounded up to the nearest integer.
Team 2’s resources and Team 1’s resources are the resource percentages. If Team 1 had all available resources in their innings and if game was not interrupted in the first innings, the denominator will be 1. (100% resources)
e.g. Rain interrupted the first innings and Team 1 used 90% of its resources to score 250. Now, rain interrupted the second inning and Team 2 has 80% resources. 250 * 0.8/0.9 will be 222.22 which means 222 is the par score and Team 2 needs 223 to win.
Scenarios: How the system works and how the score will be calculated depends on various scenarios.
- If the game is interrupted before the first innings, it would not matter because both teams will still have complete resources to score.
- In case of interruptions in the first innings but no interruptions in the second innings, the target score for Team 2 will be more than that of Team 1 to make up for the advantage that Team 2 has. This is because- if Team 1 had faced no interruptions, they could have scored more.
- In case of interruptions in the first as well as second innings, the target score will depend on whether the interruptions faced by Team 1 were more than those of Team 2 or more. Here, the percentage of resources makes sense.
- In case the second innings faces multiple interruptions, the target score is revised again and again and is lower every time.
MATH BEHIND THE RESOURCE PERCENTAGES: The D/L Model started off by assuming that the runs scored (z) are a result of an exponential decay relationship between the number of overs left and number of wickets lost. To keep matters relatively uncomplicated, we will not go into the depth of the calculations. Z0(w) is the asymptotic average runs with regards to the number of wickets lost and b(w) is the exponential decay constant.


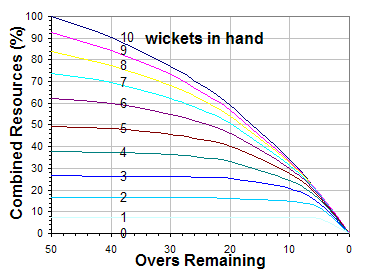
OTHER INFO: The D/L table is updated every year on 1st July. For 50 over matches decided by DLS Method, a minimum of 20 overs must be played and for 20 over games, 5 overs must be played. If the minimum number is not played, the match is declared a no result.
- Till 2003, the standard edition of the published table was used where no computer program played any role and the table was not updated regularly.

- In 2004, a new version was adopted where the resource percentage was calculated using computer software and the table was regularly updated. This version is also the “Professional Edition” which is now in use.
- In 2009, D/L method was reviewed for its use in Twenty20 matches.
- In 2015, the D/L method became the Duckworth Lewis Stern Method (DLS Method).
OTHER USES AND CRITICISM OF THE METHOD:
DLS Method is also used in:
- Ball-by-Ball Par Score: In case it is felt that the weather may interrupt the game again, the ball-by-ball par score is calculated using the D/L Method and it is shown on the scoreboard continuously.
- Net Run Rate Calculation: The NRR for a team is calculated using the DLS Method.
Criticism: The method is criticized on the grounds that the method gives a heavy weightage to wickets and thus in case of an unfavorable weather, a winning strategy would be to not lose wickets and to play at a losing rate.
Another criticism is that the D/L method does not account for changes in proportion of the innings for which field restrictions are in place compared to a completed match.
Journalists and new channels have also claimed that the method is unduly complex and hard to understand. Thus, it can be misunderstood. But after reading this blog, we can hope that you understand the method much better and cricket seems more interesting to you now. Maybe next time when the match is interrupted and DLS Method is used to calculate a target score, it would not seem as unfair and stupid. Duckworth and Lewis did use their genius and revolutionized how cricket is played even during unpredictable circumstances.
REFERENCES:
https://en.wikipedia.org/wiki/Duckworth%E2%80%93Lewis%E2%80%93Stern_method
https://www.thehindu.com/sport/cricket/in-cricket-how-does-the-dls-method-work/article27951348.ece




Amazing blog 👍🏻
LikeLiked by 1 person
💕💕
LikeLike
It’s raining sports in spring !!😀
LikeLiked by 1 person
😁😁
LikeLike
Totally loved it💯🔥
LikeLiked by 1 person
❤️❤️
LikeLike
Woah! It’s so well written😍♥️ @eloquentvee
LikeLiked by 1 person
Thank you so much 💕
LikeLike
Genuinely wow!!!!
LikeLiked by 1 person
,💕💕💕
LikeLike
Wowwww❤️❤️
LikeLiked by 1 person
❤️❤️❤️
LikeLike
Thanks a lot for the info. ! Had never clearly understood this method before you did make it simple.
LikeLiked by 1 person
I’m glad you understood. Thank you
LikeLike
Amazing!!!!
LikeLiked by 1 person
Thank you 😊
LikeLike
Amazing blog💯
LikeLiked by 1 person
❤️
LikeLiked by 1 person
too good
LikeLiked by 1 person
Thank you ❤️
LikeLike